Mathematics
Subject lead: Ms Dougall
Curriculum Intent:
Mathematics underpins much of the modern world and provides the tools to make sense of patterns, structures, and relationships. At Weavers Academy, we deliver a high-quality mathematics education designed to develop students’ curiosity, logical reasoning, and problem-solving skills so that they are equipped to interpret and model the world around them, think critically, and become confident, numerate global citizens.
Specialist subject leaders from across all CET secondary academies have collaborated to construct a Mathematics curriculum that is ambitious and meets the needs of our students. The Mathematics leadership team at Weavers Academy has adapted a curriculum for our specific context. At its core, our spiralling curriculum is knowledge-rich, ensuring students acquire the essential concepts and techniques needed to succeed in mathematics. Alongside this, authentic and diverse content is woven into our curriculum to ensure all students feel a sense of belonging and engagement throughout their learning journey.
Our knowledge-rich approach is supported by robust assessment practices. Summative end-of-unit assessments are complemented by annual assessments, which inform curriculum design and evaluate impact at topic level. These assessments are designed by subject leaders at our Academy and informed by best practice shared across our sister schools.
As students progress through their mathematical education, they will apply mathematical reasoning and vocabulary to solve a wide range of problems, develop fluency in core skills, and use their analytical abilities to interpret data and justify conclusions. They will also learn to critically evaluate solutions and communicate their reasoning effectively.
The Weavers Academy Mathematics Department has high expectations of all learners and is committed to our Academy’s PRIDE values:
-
Productivity: Students are supported to consistently produce work that exceeds expectations relative to their target grades.
-
Determination: Students are encouraged to persevere when faced with challenging problems.
-
Independence: Students are empowered to work effectively both collaboratively and independently, ultimately achieving strong outcomes in external assessments.
-
Engagement: Our tailored, knowledge-rich curriculum stimulates high levels of engagement, while authentic diversity threads ensure all students feel a sense of belonging.
-
Respect: Students show respect for themselves and others throughout their learning journey.
Curriculum Aims
The Weavers Academy Mathematics curriculum aims to ensure that all pupils:
-
Have their individual needs considered and supported, including those from disadvantaged backgrounds and with SEND.
-
Benefit from carefully sequenced, knowledge-rich concepts that lead to deep learning through our bespoke spiral curriculum.
-
Develop confidence and competence in applying mathematical methods and reasoning.
-
Become proficient in problem-solving and logical thinking.
-
Engage in mathematical discussion and debate, justifying solutions and exploring alternative approaches.
-
Develop resilience and confidence when tackling unfamiliar problems.
-
Become mathematically literate, able to interpret and question data and information in everyday life.
-
Experience mathematical cultural capital throughout the curriculum.
-
Understand the range of careers that require mathematical skills and make explicit connections between content studied and future opportunities.
Home Learning
Is set and completed on Sparx each week from Wednesday to Wednesday. This provides a vital part of our learning cycle allowing pupils access to expert videos and personalised support through the curriculum.
Click here for guidance on how to access Sparx
Key Stage 3:
Our spiral curriculum revisits and builds upon fundamental concepts first encountered at Key Stage 2. Key ideas are revisited each year with increasing complexity. Students develop fluency in number, algebra, geometry, and data handling, while applying these skills to solve problems. They learn to reason mathematically, construct arguments, and interpret results, supported by opportunities to apply mathematics in real-world contexts.
Year 7 Curriculum Map:
| Autumn 1 |
7.01 Directed numbers |
|
7.02 Number properties |
|
|
7.03 Order of operations |
|
| Autumn 2 |
7.04 Powers of 10 and decimal arithmetic |
|
7.05 Representations of Fractions |
|
|
7.06 Introduction to algebra |
|
| Spring 1 |
7.07 Fractions (4 operations) |
|
7.08 FDP |
|
| Spring 2 |
7.09 Solving equations |
|
7.10 Averages |
|
|
7.11 Angles and properties of 2D shapes |
|
| Summer 1 |
7.12 Units |
|
7.13 Area and perimeter |
|
| Summer 2 |
7.14 Probability of events |
|
7.15 Co-ordinates |
|
|
7.16 Statistical graphs |
Year 8 Curriculum Map:
| Autumn 1 | 8.01 Index laws |
| 8.02 Algebraic expressions | |
| 8.03 Fractions | |
| Autumn 2 | 8.04 Solving Equations |
| 8.05 Rounding and Estimating | |
| 8.06 Circles | |
| 8.07 Sequences | |
| Spring 1 | 8.08 Ratio |
| 8.09 3D shapes and Volume | |
| Spring 2 | 8.10 Pythagoras' theorem |
| 8.11 Direct and Inverse proportion | |
| 8.12 Pie charts | |
| Summer 1 | 8.13 Percentages |
| 8.14 Angles in parallel lines | |
| Summer 2 | 8.15 Probability trees |
| 8.16 LCM & HCF | |
| 8.17 Scatter graphs |
Year 9 Curriculum Map:
| Autumn 1 | 9.01 Decimals |
| 9.02 Rounding and bounds | |
| 9.03 Compound measures | |
| Autumn 2 | 9.04 Algebraic expressions |
| 9.05 Changing the subject | |
| 9.06 Right-angled trigonometry | |
| 9.07 Surface areas | |
| Spring 1 | 9.08 Linear and Quadratic graphs |
| 9.09 Standard form | |
| Spring 2 | 9.10 Transformations |
| 9.11 Percentages | |
| 9.12 Angles in polygons | |
| Summer 1 | 9.13 Algebraic proportion |
| 9.14 Venn diagrams | |
| Summer 2 | 9.15 Congruence, Similarity and Constructions |
| 9.16 Scale drawings and bearings |
Key Stage 4:
GCSE Mathematics
Specification: https://filestore.aqa.org.uk/resources/mathematics/specifications/AQA-8300-SP-2015.PDF
At Key Stage 4, students deepen their understanding of mathematical concepts and processes, developing fluency and confidence across all areas of the GCSE specification. The curriculum equips students with the mathematical knowledge required to understand and apply mathematics in a range of contexts, both now and in the future. Students learn to model situations mathematically, interpret results, and communicate solutions effectively.
Foundation Curriculum Map:
| Term | Year 10 Foundation | Year 11 Foundation |
|
Autumn 1 |
10.01 Indices and roots 10.02 Fundamentals of algebra 10.03 Forming and solving equations |
11.01 HCF LCM 11.02 Fractions percentages 11.03 Plans and elevations 11.04 Angles and bearings |
| Autumn 2 |
10.04 Simultaneous equations 10.05 Right-angled triangles |
11.05 Statistical graphs 11.06 Functions 11.07 Loci |
| Spring 1 |
10.06 Similarity and congruence 10.07 Transformations 10.08 Circles |
11.08 Non-linear graphs 11.09 Standard form 11.10 Sequences |
| Spring 2 |
10.09 Coordinates and linear graphs 10.10 Ratio 10.11 Averages |
11.12 Proportion 11.13 Vectors |
| Summer 1 |
10.12 Probability 10.13 Inequalities 10.14 Volume and surface area |
|
| Summer 2 |
10.15 Compound measures and rounding 10.16 Probability diagrams |
Higher Curriculum Map:
| Term | Year 10 Higher | Year 11 Higher |
|
Autumn 1 |
10.01 Indices and surds 10.02 Advanced trigonometry |
11.01 Algebraic fractions 11.02 Identities and Proofs 11.03 Statistical Graphs |
| Autumn 2 |
10.03 Quadratics 10.04 Averages and Scatter graphs 10.05 Simultaneous equations |
11.04 Circle theorems 11.05 Functions and Iterations |
| Spring 1 |
10.06 Bearings, Construction and Loci 10.07 Arcs, Sectors and Segments 10.08 Linear Graphs |
11.06 Vectors 11.07 Graphs and transformation of graphs 11.08 Sequences |
| Spring 2 |
10.09 Ratio and proportion 10.10 Congruence and Similarity 10.11 Probability |
11.09 Area under and gradient of a curve 11.10 Tangent to a circle |
| Summer 1 |
10.12 Equations and inequalities 10.13 Transformations 10.14 Volume and surface area |
|
| Summer 2 |
10.15 Growth ad decay 10.16 Advanced number 10.17 Compound measures |
Key Stage 5:
A-Level Mathematics
Specification: https://qualifications.pearson.com/en/qualifications/edexcel-a-levels/mathematics-2017.html
At Key Stage 5, students further develop their mathematical reasoning and problem-solving skills through advanced study. They gain a deep understanding of mathematical structures and techniques, preparing them for progression to Higher Education and careers requiring strong mathematical competence.
Year 12 Curriculum Map:
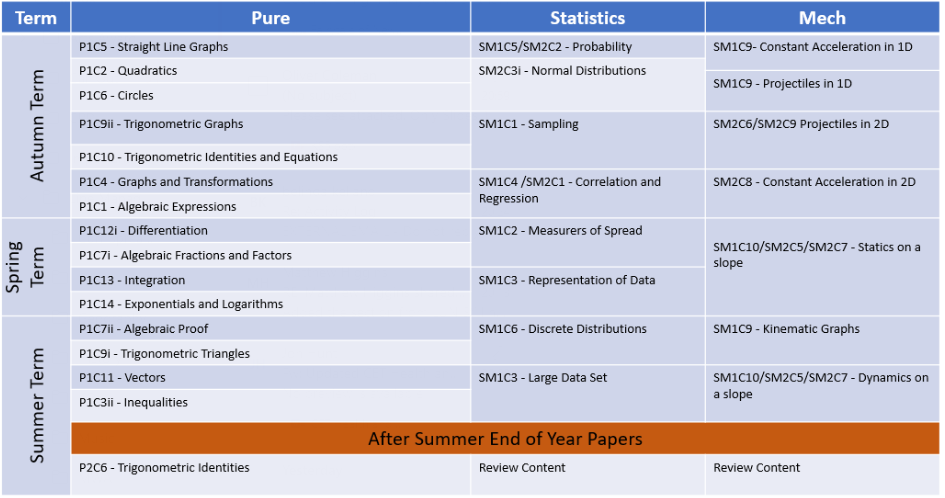
Year 13 Curriculum Map:
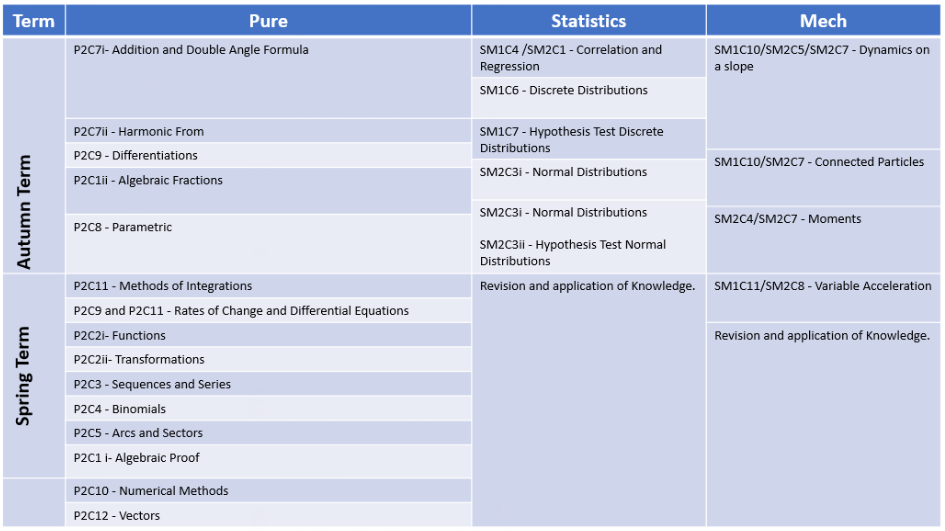
Students enjoy a range of places to be able to access resources and support locations. These are all directly link to the PLCs and text book.
- On Teams in the WEA – A-Level team
- https://integralmaths.org/ – Great Videos about each topic. Please see your Maths Teacher for Details.
- Videos explaining Each Example from the Text book (kindly shared by Haberdashers’ Adams): https://www.youtube.com/channel/UCyyRmnmtgVy5Sm7_UiCLFgQ/playlists
- https://www.physicsandmathstutor.com/maths-revision/a-level-edexcel/ (and revision notes)
- https://www.westiesworkshop.com/course-support/
- https://alevelmathsrevision.com/maths-categorised-exam-questions/
- https://www.savemyexams.co.uk/a-level/maths/
- https://www.madasmaths.com/ (Some of these question can be beyond the specification but are good to extend yourself with)
- https://www.examsolutions.net/alevel-exam-boards/edexcel/
Enrichment
Pupils are taught and participate in the UK Maths challenge to develop lateral thinking and further work

